作者：桂。

时间：2017-06-03  21:46:59

链接： 

原文下载：

---

前言

1982年的文章了，主要是基于GSC框架的麦克风阵列增强，梳理一下文章的思路。这篇文章主要有两点特色：

　　1）在基础上，进行了理论扩展;

　　2）论述了基于麦克风阵列的GSC框架.

一、理论回顾

假设噪声为加性：

其中s是desired signal,n 是noise.m为第m个麦克风，m∈[1,M].

加权的beamforming可以写为

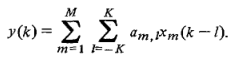
滤波器的抽头长度为2K+1.对应的框架为：

上面的定义式可以进一步简化，根据

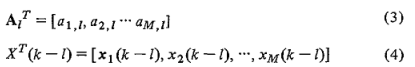
输出为

 

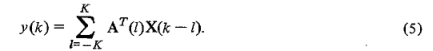
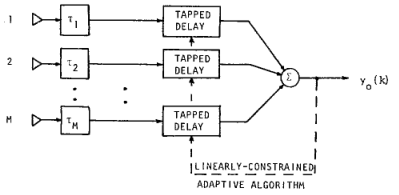
实现结构知道了，下面就是定义目标函数，然后就是理论的落地，具体可以参考。细节上的改动可以看原文，个人觉得对于实际应用影响可以忽略。

二、GSC框架

 GSC的理论推导。它本质上也是LCMV的应用，不同之处在于：假设C为M×L的矩阵：L个线性约束条件。对于M个变量的方程组，对应唯一解最多有M个方程，即：对于L个线性约束来讲，我们仍可以继续利用剩下的M-L个自由度进行约束，使得结果更加符合需求，这便是GSC的意义。可以说GSC是MVDR的强化版，但效果是不是一定最优难以保证，例如MVDR是最优权重，而GSC上支的增强向量、下支的Block矩阵通常直接给定，只是优化LMS中的权重。

GSC的描述：

　　The GSC algorithm is comprised of three building blocks. The first is a fixed beamformer, which satisfies the desired constraint. The second is a blocking matrix, which produces noise-only reference signals by blocking the desired signal (e.g., by subtracting pairs of time-aligned signals). The third is an unconstrained LMS-type algorithm that attempts to cancel the noise in the fixed beamformer output.

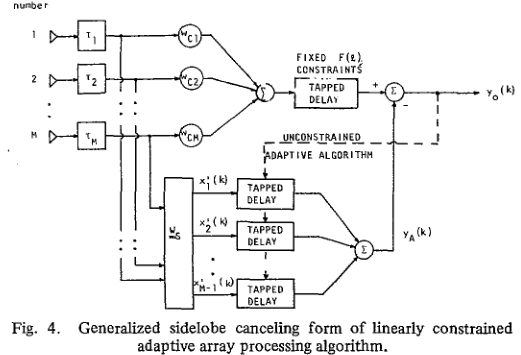
简单说一下实现思路：仍然可以按频点处理，首先是延迟t的估计，然后是对齐，上支是叠加/下支是block，这样一来上支看成是目标信号带有噪声，下支看成是噪声，从而利用自适应滤波的思想对上支信号进行降噪。假设麦克风为M个，滤波的抽头系数为2K+1，借助梯度下降的思想，这样便完成了理论的落地，实现了工程应用。具体的思路与Frost's algorithm中的思路基本一致，不再赘述。

 

参考

• Griffiths L, Jim C W. An alternative approach to linearly constrained adaptive beamforming[J]. IEEE Transactions on antennas and propagation, 1982, 30(1): 27-34.